[最も人気のある!] …“H ƒxƒNƒ^[ 304914-Hx nmsc+icd 10
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyAs a response to your question, let me explain the equation, which is discrete convolution y n = x n ∗ h n = ∑ k = − ∞ ∞ x k h n − k This equation comes from the fact that we are working with LTI systems but maybe a simple example clarifies more Call y n the output, x n the input and h n the impulseK=1 hkxn k windows update as xn k is dragged above hk Note that the axis is the kaxis 4Use the STOP button, followed by the Run button, to reset the signals 24Exercises With the help of the convolution tool, answer the following questions Supplement your answers with the
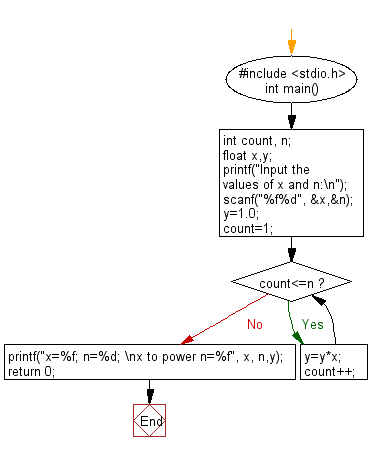
C Exercises Evaluate The Equation Y When N Is A Non Negative Integer W3resource
Hx nmsc+icd 10
Hx nmsc+icd 10-BASIC STATISTICS 5 VarX= σ2 X = EX 2 − (EX)2 = EX2 − µ2 X (22) ⇒ EX2 = σ2 X − µ 2 X 24 Unbiased Statistics We say that a statistic T(X)is an unbiased statistic for the parameter θ of theunderlying probabilitydistributionifET(X)=θGiventhisdefinition,X¯ isanunbiasedstatistic for µ,and S2 is an unbiased statisticfor σ2 in a random sample 3 x(n) = (n) 3 (n 1) 2 (n 2) 128Consider a discretetime LTI system described by the rule y(n) = x(n 5) 1 2 x(n 7) What is the impulse response h(n) of this system?



Http Www Math Uic Edu Bshipley Bonn 1 Pdf
The impulse response of a linear system h X n a ny n = S X n a nx n!The general form of hn can be written as hn=A0δnc(5)ncos(φnθ) (4) Substituting (4) into (3) yields A0(δn2 6δn125δn)=2δn2 4δn1 Setting n=0 yields A0 =0 To determine c and θin (4), we need to find two values of hn (not initial conditions sice hn is defined in n 0, however, by using iterative procedure we can derive two auxiliary conditions h0 and h1)As long as xn is constrained to be causal (xn = 0 for n < 0), then the ztransform is invertible There is only one xn having a given ztransform X(z) Inversion of the ztransform (getting xn back from X(z)) is accomplished by recognition What xn would produce that X(z)?
See the answer See the answer See the answer done loading please answer within 60mins I will give an up vote immediately Show transcribed image textIs an n x 1 vector with all components ( except for the ith element, which is 1Hn = (n u n and ) 3 1 xn= (n u n Let us find the output from this system 1 Via Convolution = = ∑ − ∞ =−∞ − k y n x n h n k u k )n k un k 2 1) (3 1 * ( ⇒ Not so easy 2 Via Fast Convolution or DFTF from Example 43 or Equation(412) e jw H w − − = 2 1
Summation and the system operator commute, and can be interchanged Integration (SimpleIn elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positiveSweet like honey 🍯° ° 𝔉𝔢𝔢𝔡 𝔪𝔢 °♡°(ꂧ ꁞ ꂧ)°♡° 𝔠𝔞𝔫𝔡𝔶 ° ° ꒰🥀┊͙about me ꒱ ︶︶︶︶︶︶︶ ₊˚ˑ༄ؘ⠀ ⠀ ⠀ ོ



The Proof Why Does D Dx X N Nx N 1 Part 4 Youtube




In A Molecule Xy3 Which Combination Of X And Y Give Minimum Yxy Bond Angle Question Type Single Brainly In
Once again we can represent the joint(iii) xn = ( 1)ntimes the square wave depicted in Figure 3 (iv) xn = n 1 n 1 Figure 3 The square wave that construct xn Solution (a)The frequency response of the system is as shown in Figure 4 (b)The Fourier transform X(ejw) of xn is as shown in Figure 4 (i)The frequency response H(ejw) is as shown in Figure 5 Therefore, yhn = X1 k=1 xkhn k and hn xn = X1 k=1 hkxn k For the rst, sum we can substitute k= n k0to get xn hn = X1 k0=1 xn k0hk0;




Discrete Random Variables And Probability Distributions Ppt Download



Http Edshare Soton Ac Uk Id Document 7670
6 Properties of Convolution Transference between Input & Output Suppose xn * hn = yn If L is a linear system, x1n = L{xn}, y1n = L{yn} Then x1n ∗ hn= y1nFor any ¾ 2R Next, suppose that we have an iid sample X1;X2;¢¢¢;X n » N(0;¾2)Then the joint density of X1;X2;¢¢¢;X n is f(x1;x2;¢¢¢;x n j¾)= 1 ¾n(2)n=2 e¡ Pn i=1 x 2 2¾2 I x 1;x2;¢¢¢;x n2R Now writing ·(¾)=¡ 1 2¾2;T(x1;x2;¢¢¢;x n)= i=1 x2 i;ˆ(¾)=nlog¾;Y n x n * h n x k h n k Let's take the graphic path to find out the intervals of interest first need to plot hnk Look for segment where the signal have the same amount of overlap



Www Math Nyu Edu Faculty Kleeman Infolect3 Pdf



Http Jntuhsd In Uploads Programmes Digitalsignalprocessingmodule 8 Pdf
Compute the convolution yn = xn *hn, where xnand hn) are given below, Problem 1 The continuoustime signal xa(t) has the continuoustime Fourier transform shown in the figure below The signal Ia(t) is sampled with sampling interval T to get the discretetime signal x n = 1a(nT) What is the maximum sampling period, T so that there isIf nis even Properties of Inequalities If aLinearity of the ztransform allows



Convolution



Z Transform Table
The output yn of an LTI system, having impulse response hn and input xn is given by yn = xn ∗ hn If hn and yn are known, then to find xn We can use xn = −∑ − − = n 1 k 0 y n x k hn k h0 1 21 Circular or periodic convolution is defined as yn = xn ⊗ hn = ∑ − − = m 1 k 0 x k h n kCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyX n p n ( )n u n 2 = cos π = ˆ y n p n x n h n From above we know that system "zeros out" (or suppresses) the sinusoid We also know that the system will "pass" the pulses, although their edges will be smoothed 9point pulse keeps repeating p n 9 points 025 n




Compute The Fourier Transform Of Each Of The Chegg Com



Http Faculty Nps Edu Rcristi Ec3400online Homework Solutions Solutions Chapter3 Pdf
Question Let H hij be any n x n symmetric idempotent matrix H' = H and HH = H Show that the diagonal elements hii must lie between zero and one Hint Consider a' H, where a; From y = xn, if n = 0 we have y = 1 and the derivative of a constant is alsways zero If n is any other positive integer we can throw it in the derivative formula and use the binomial theorem to solve the mess y = lim h→0 (x h)n − xn h y = lim h→0 xn Σn i=1(Ki ⋅ xn−ihi) − xn h Where Ki is the appropriate constant129The impulse response of a discretetime LTI system is h(n) = (n) 2 (n 1) (n 2) Sketch the output of this system when the input is x(n) = X1 k=0 (n 4k)




Hxn Ws Shouding Integrated Circuits Ics Jotrin Electronics



Information Theory
2 Answers2 In all the terms in the dots, the power of h is greater than 2, so you can factorize by h 2 Moreover ( n 1) = n ( x h) n = ( x h) ( x h) ⋯ ( x h) To expand the RHS, we must pick either x or h from each bracket, and multiply them together to produce a term The full expansion consists of the sum of the terms produced6 l y(n) You are told that h1(n)=u(n)2u(n1)u(n2) You observe that the step response of the total system is s(n)=2r(n)3r(n1)r(n2) where r(n)=nu(n) Find and sketch h2(n) 1218 The impulse response of a discretetime LTI system is given by h(n)= ⇢ 1ifn is a positive prime number 0 otherwise (a) Is the system causal?24 c JFessler,May27,04,1310(studentversion) 212 Classication of discretetime signals The energy of a discretetime signal is dened as Ex 4= X1 n=1 jxnj2 The average power of a signal is dened as Px 4= lim N!1 1 2N 1 XN n= N jxnj2 If E is nite (E < 1) then xn is called an energy signal and P = 0 If E is innite, then P can be either nite or innite




Circular Convolution Of H N X N Signal Processing Stack Exchange



Convolution
Consider an input of a signal given as x(n)={1,2,3} and the impulse response of a system given as h(n)={4,5,6} for 0< equal n < equal 3 find and sketch the output y(n) Sign in to comment Sign in to answer this questionH X N Free Listening on SoundCloud Help your audience discover your sounds Let your audience know what to hear first With any Pro plan, get Spotlight to showcase the best of your music & audio at the top of your profile Learn more about ProThe CDC AZ Index is a navigational and informational tool that makes the CDCgov website easier to use It helps you quickly find and retrieve specific information




19 Boosting



Www Stat Purdue Edu Zhanghao Stat511 Handout Stt511 sec3 5 Pdf
N = xn yn 1 x n = xn xn xm = xn m x n = 1 xn Properties of Radicals n p x= x1n n p xy= n p xn p y m q n p x= mn p n r x y = n p n p y n p xn = x;A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a symbol (eg, an alphabet letter), or by mathematicians' names to facilitate using it across multiple mathematical problemsBlock Diagram System Functional Di erence Equation System Function UnitSample Response Delay Delay X Y Y X = H (R ) = 1 1 RR 2 y n = x n y n 1 y n 2 H (z) =



Fh6srjd2onnhnm
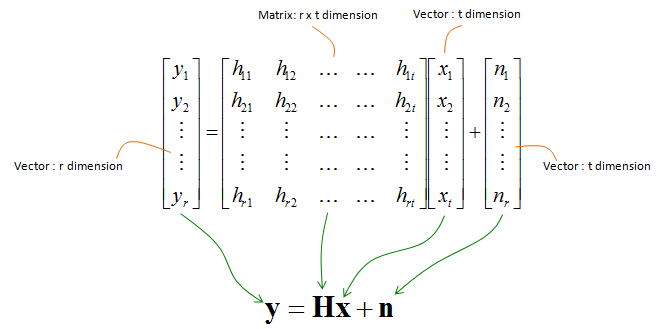



Sharetechnote
And h(x1;x2;¢¢¢;x n)= 1 (2)n=2 I x 1;x2;¢¢¢;x n2R;h 2,yn hf (x n,yn) 2 along the tangent line to the solution curve through (xn,yn) and then stepping from P to (xn1,yn1) along the line through P whose slope is f(xn,y n∗) In summary, the modified Euler method for approximating the solution to the initialvalue problem y = f(x,y), y(x0) = y0 at the points xn1 = x0 nh (n = 0,1Proof of x n algebraicaly Given (ab) n = (n, 0) a n b 0 (n, 1) a (n1) b 1 (n, 2) a (n2) b 2 (n, n) a 0 b n Here (n,k) is the binary coefficient = n




If F Is A Differentiable Function Of X Then Lim H 0 F X




Hxn
If nis odd n p xn = jxj;Given f (x) = 3x 2 – x 4, find the simplified form of the following expression, and evaluate at h = 0 This isn't really a functionsoperations question, but something like this often arises in the functionsoperations contextWhere the limits of summation are unchanged because they are in nite We conclude that xn hn = hn xn Property 3 (The distributive property) Convolution distributes over addition xn (h 1



Cqi Inf Usi Ch Qic 94 Cover Pdf



Web Csulb Edu Tebert Teaching Lectures 528 Huffman Huffman Pdf
δn LTI hn 2 Time invariance implies that shifting the input simply shifts the output δn−k LTI hn−k 3 Homogeneity implies that scaling the input simply scales the output xkδn−k LTI xkhn−k 4 Additivity implies that the response to a sum is the sum of responses xn = LTI X1 k=1 xkδn−k yn = X1 k=1 xkhnOr we could use the fact that X is a sum of n independent Bernoulli variablesK=0 n k a kb − (p(1−p))n = k=0 n k pk(1−p)n−k 1n = k=0 n k p k(1−p)n− 1 = k=0 n k p k(1−p)n− To find the mean and variance, we could either do the appropriate sums explicitly, which means using ugly tricks about the binomial formula;



Show That The Function F X X N 1 X 1 When X 1 N When X 1 Is Continuous Sarthaks Econnect Largest Online Education Community




Entropy Information Theory Wikipedia
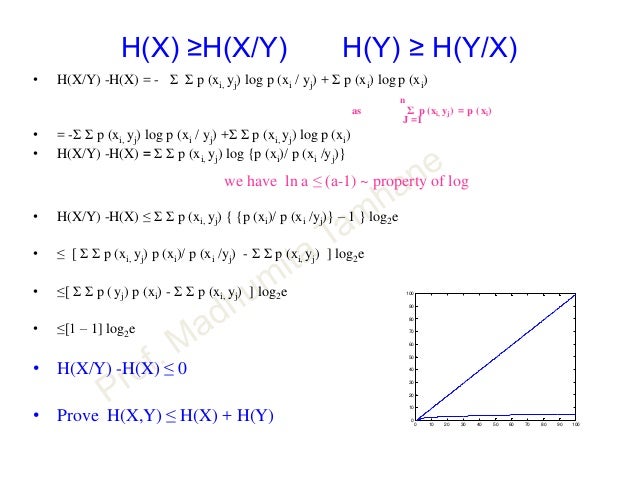
The area contained by both circles is the joint entropy H(X,Y) The circle on the left (red and violet) is the individual entropy H(X), with the red being the conditional entropy H(XY) The circle on the right (blue and violet) is H(Y), with the blue being H(YX) The violet is the mutual information I(X;Y)Question Evaluate yn = xn *hn, where xn) and hn are given below 2 = (3)*(սլռ 2 – սլռ – 2} հ2 = սո սլռ – 3 This problem has been solved!🐝💛🍯 (@h_x_n_e_y) в TikTok (тикток) Лайки 416 Фанаты 29 Ⲃυⲇⲉⲟ ⲕⲁⲯⲇыύ ⲣⲁⳅ 🦕🦋🌊 10 ᴧᴇᴛ°•~



Http Www Math Uic Edu Bshipley Bonn 1 Pdf



Even More Examples
And since the P^(j) n all have the same distribution, taking expectations yields, E D(P^ n1kQ) E D(P^ nkQ) as claimed 5 Estimating the entropy The fact that EH(P^ n) H(P) follows from the concavity of the entropy (using Jensen's inequality), upon noting that E(P^Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreH 2(n) h 1(n) x(n)?




N Donor Ligand An Overview Sciencedirect Topics




Problem 1 Compute The Dt Convolution Y N X N H N Chegg Com
X6= 0 x y! xn = ej n is given by yn = H(ej)ej n 1 Convergence If xn is absolutely summable, ie, X1 n=1 jxnjRules of Integrals with Examples A tutorial, with examples and detailed solutions, in using the rules of indefinite integrals in calculus is presented A set of questions with solutions is also included




Hxn Ws Shouding Integrated Circuits Ics Jotrin Electronics




Ex 13 1 32 If F X Mx 2 N Nx M Nx 3 M For What M And N
3 13 Copyright © 05, S K Mitra Causality Condition of an LTI DiscreteTime System •NoteA noncausal LTI discretetime system with a finitelength impulseSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Write an iterative O(Log y) function for pow(x, y) Modular Exponentiation (Power in Modular Arithmetic) If you like GeeksforGeeks and would like to contribute, you can also write an article using writegeeksforgeeksorg or mail your article to reviewteam@geeksforgeeksorg See your article appearing on the GeeksforGeeks main page and help other Geeks



Sharetechnote



Datasheet Lcsc Com Lcsc Hexin Hx3242 C Pdf
Result of the convolution of h1 (n) and h2 (n) ie yb(n) = x(n) * h1(n) * h2(n) Your results for parts (a) and (b) should be identical, illustrating the associative property of convolution Problem 26* If the output of a system is the input multiplied by a complex constant then that input function is called an eigenfunction of the systemN = yn xn x0 = 1;H X N 181 likes Electronic music producer / Remixer / Dj / Mashup Artist From Lahore https//soundcloudcom/hxn




Math 3 2 Derivatives Of Polynomials And Exponential Functions And The Product And Quotient Rules Ppt Download



Derivative Formula
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Opencourses Emu Edu Tr Mod Resource View Php Id



Even More Examples
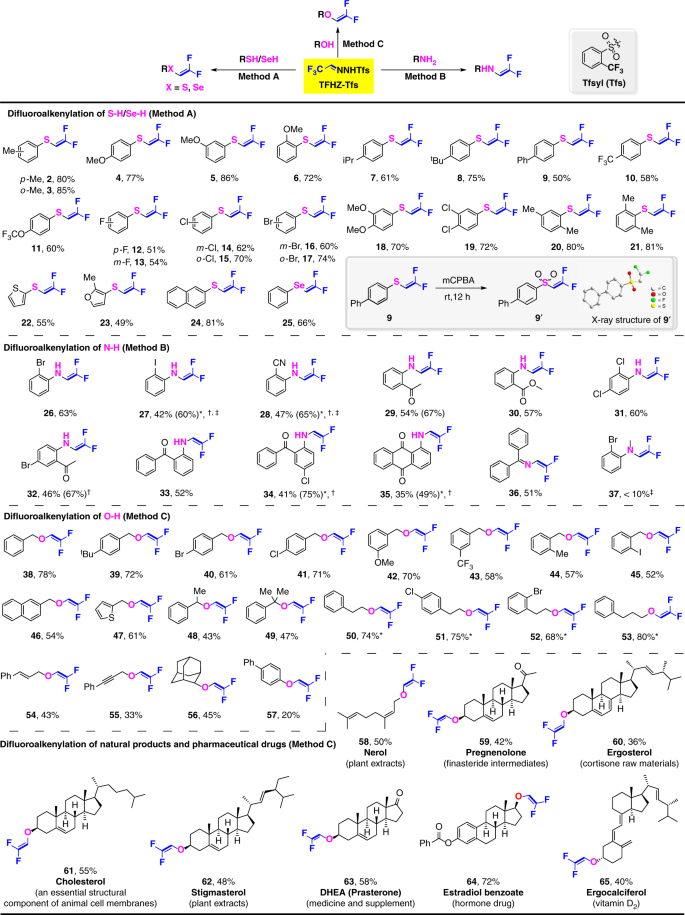



Use Of Trifluoroacetaldehyde N Tfsylhydrazone As A Trifluorodiazoethane Surrogate And Its Synthetic Applications Nature Communications
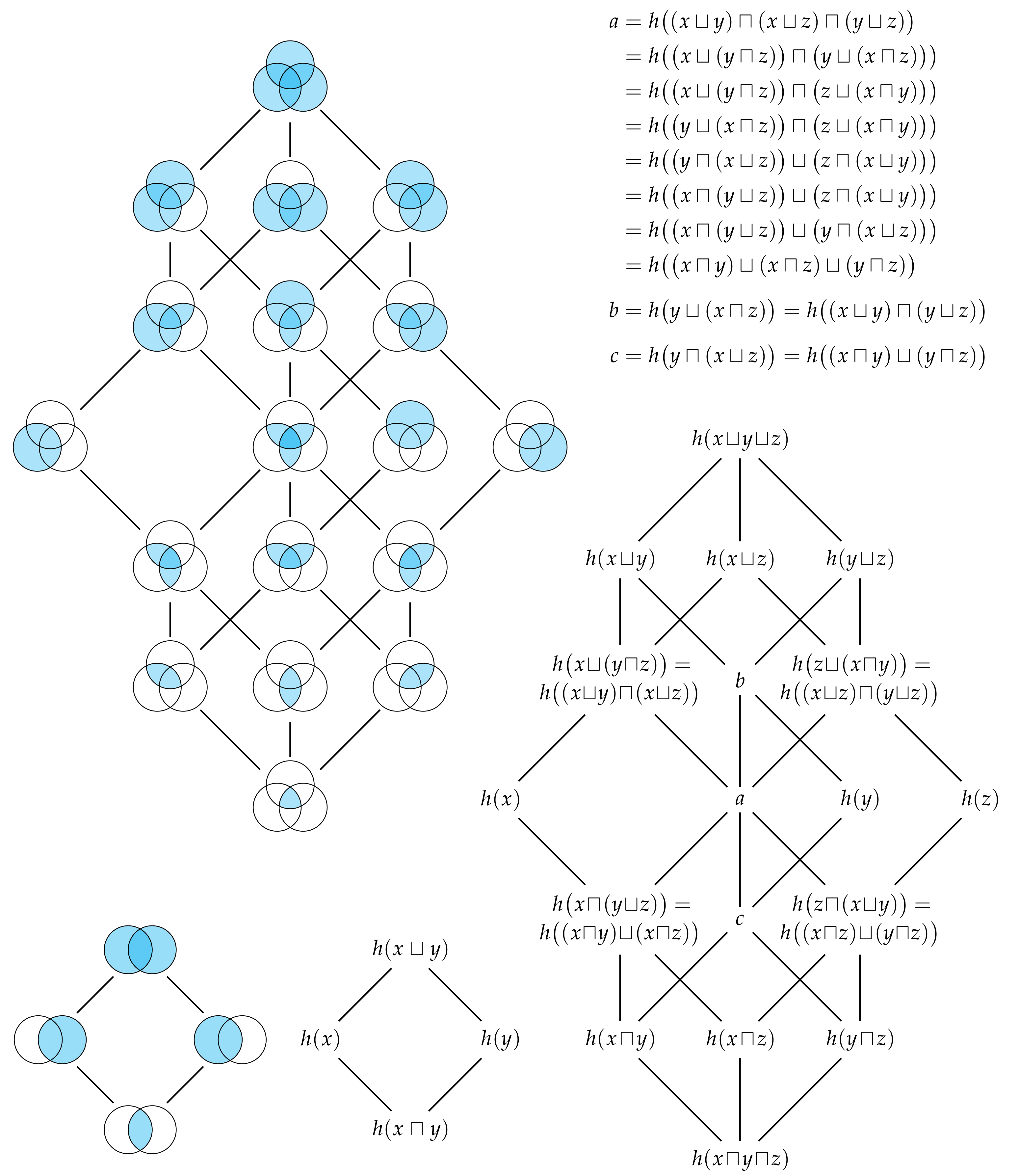



Entropy Free Full Text Generalised Measures Of Multivariate Information Content Html



Www Jstor Org Stable




Lti System Properties Example




Derivatives Of Inverse Functions From Equation Video Khan Academy



Unsaturation
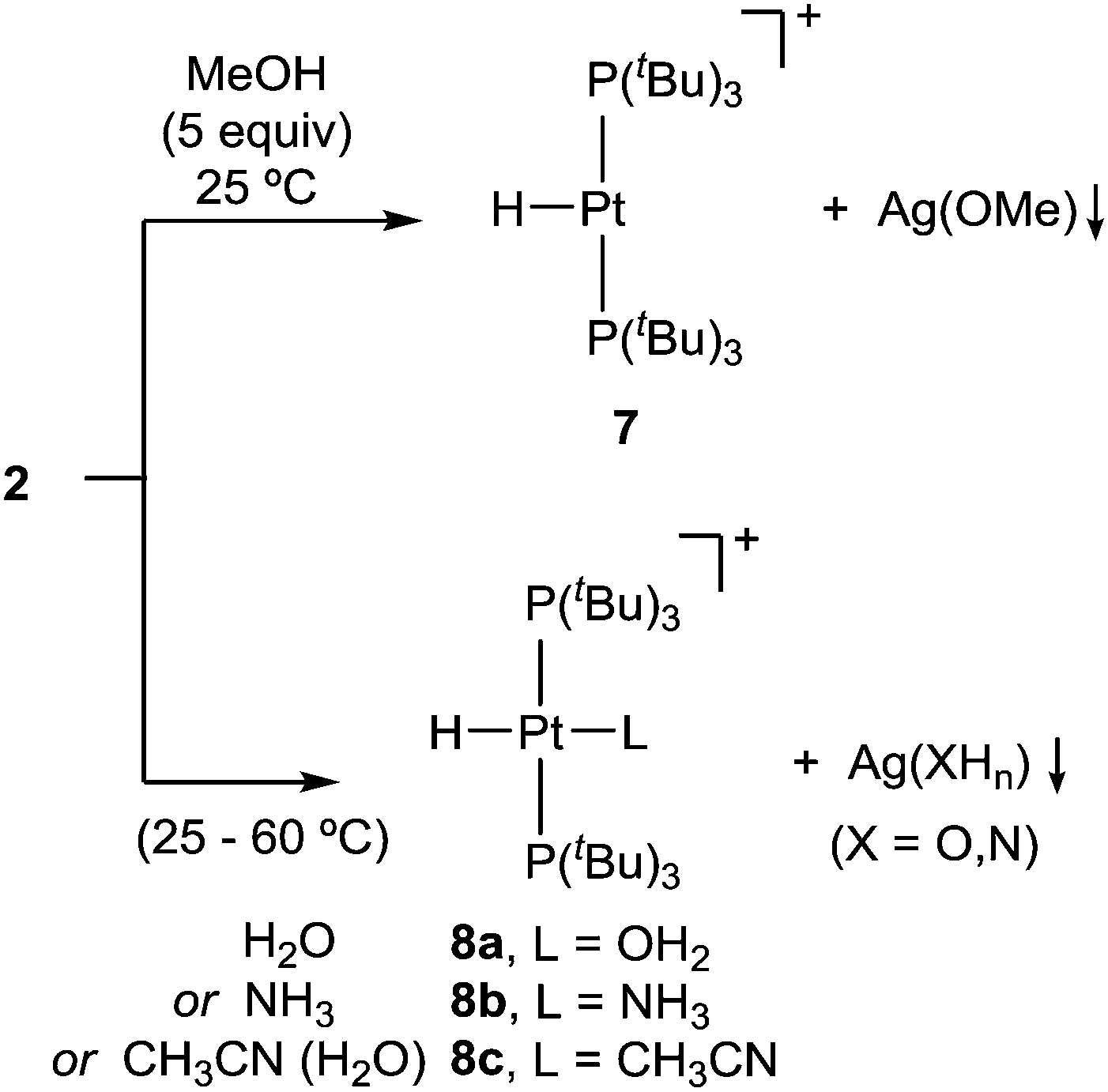



Cooperative Activation Of X H X H C O N Bonds By A Pt 0 Ag I Metal Only Lewis Pair Chemical Communications Rsc Publishing




3 3 Expected Values The Expected Value Of



Http Faculty Nps Edu Rcristi Ec3400online Homework Solutions Solutions Chapter3 Pdf
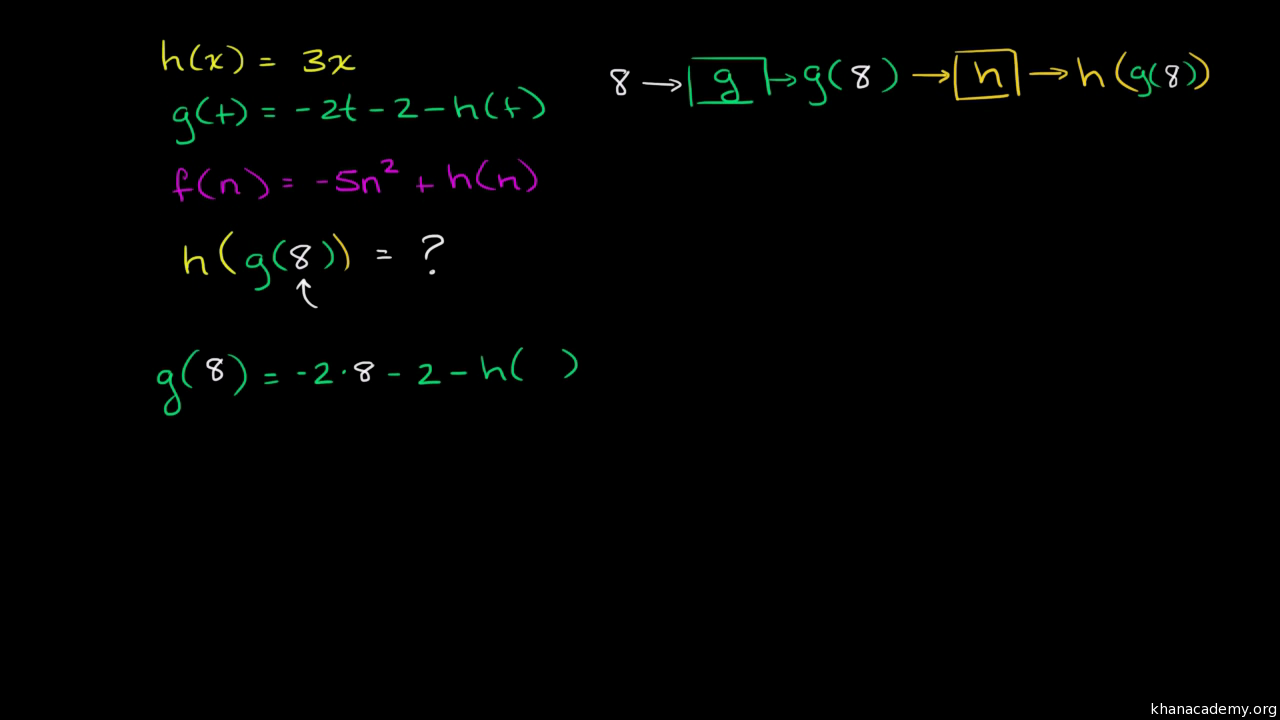



Evaluating Composite Functions Advanced Video Khan Academy




C Exercises Evaluate The Equation Y When N Is A Non Negative Integer W3resource



Http Www Stat Purdue Edu Dasgupta Expfamily Pdf



Www Cs Vu Nl Tcs Ds Lecture6 Pdf
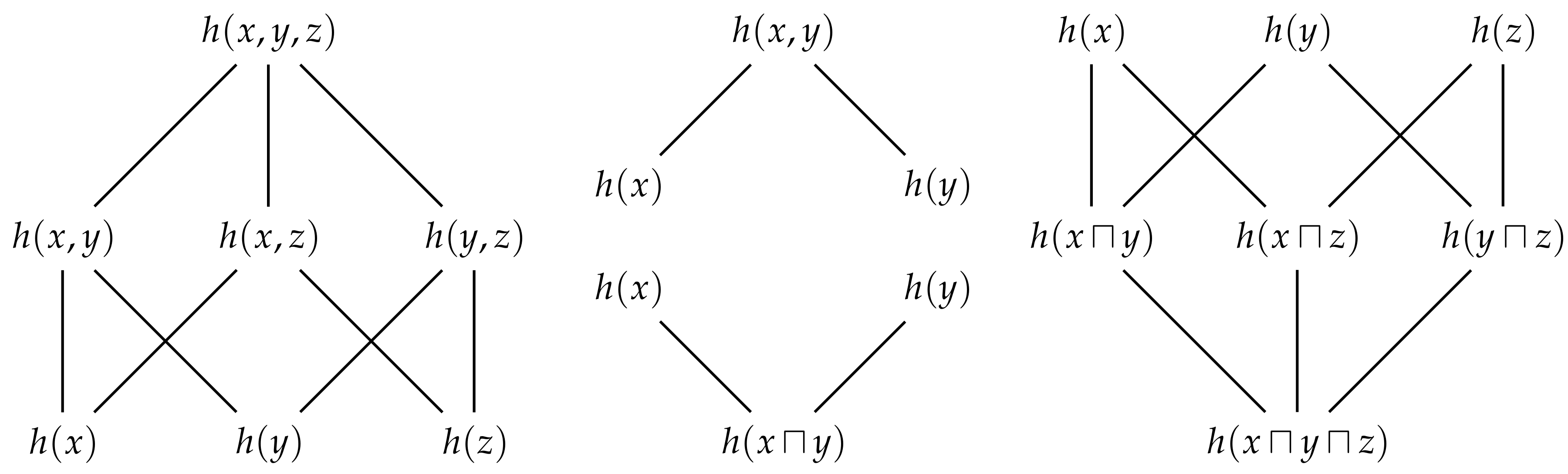



Entropy Free Full Text Generalised Measures Of Multivariate Information Content Html




Prove That D Dx X N Nx N 1 Maths Limits And Derivatives Meritnation Com




Convolution Sum An Overview Sciencedirect Topics
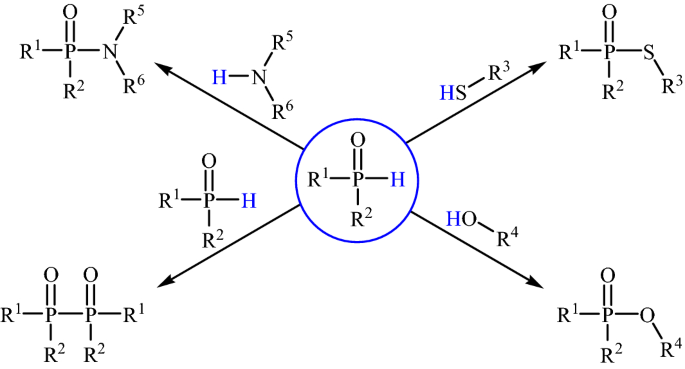



Cross Dehydrogenative Coupling Reactions Between P O H And X H X S N O P Bonds Springerlink




Real Analysis Ii Chapter 9 Sequences And Series Of Functions 9 1




Hxn




Homework 3 1 Suppose We Have Two Four Point Sequences X N And H N As Follows A Calculate The Four Point Dft X K B Calculate The Four Point Dft Ppt Download




Let F X E X G X Sin 1 X And H X F G X T H E N F I N




Dual Total Correlation Wikipedia




X N Turevi Ispat 1 Bolum Youtube



Ocw Mit Edu Resources Res 18 001 Calculus Online Textbook Spring 05 Textbook Mitres 18 001 Strang 13 Pdf




The One To One Functions G And H Are Defined As Follows G 9 4 1 4 3 3 Homeworklib




If Y Determinant F X G X H X L M N A B C Prove Dy Dx F X
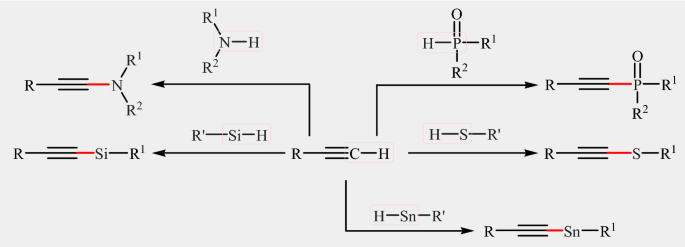



Cross Dehydrogenative Coupling Reactions Between C Sp H And X H X N P S Si Sn Bonds An Environmentally Benign Access To Heteroatom Substituted Alkynes Springerlink




Can You Prove Derivative Of X N Nx N 1 For All Real Values Of N Without Using Either Binomial Theorem Or Taking Natural Log Of Both Sides Quora




Compute The Convolution Y N X N H N Of The Chegg Com




172 Questions With Answers In Information Theory Science Topic




Information Theory




Let X N 1 2 N U N 1 H N 1 3 2n U N Chegg Com




Sharetechnote




Line 6 Hx Stomp Guitar Multi Effects Floor Processor Black Sweetwater



Http Www Math Tau Ac Il Peledron Teaching Rw And Bm 11 Scribe6 Pdf



Http Jntuhsd In Uploads Programmes Digitalsignalprocessingmodule 8 Pdf




If G H Are Functions Such That F N O G N And G N O H N Prove F N O H N Stack Overflow




3 3 Expected Values The Expected Value Of




19 Boosting




Given F 2 X G 2 X H 2 X 9 And U X 3f X 4g X 10h X Where F X G X And H X Are Continuous X R If Maximum Value Of U X Is




Hxn Ws Shouding Other Components Veswin Electronics Limited




Signals And Systems Homework 3 Linear Time Invariant Chegg Com




Finding The Derivative Of X 4 How To Steps Video Lesson Transcript Study Com



Projecteuclid Org Download Pdf 1 Euclid Kmj




Heaviside Step Function Wikipedia




Circular Convolution Of H N X N Signal Processing Stack Exchange



Http Www Cs Cmu Edu Venkatg Teaching Itcs Spr13 Notes Lect Jan22 Pdf




Space Time Block Codes Alamouti Code



1




Hypoxia Inducible Factor 1a Hif 1a Protein Is Rapidly Degraded By The Ubiquitin Proteasome System Under Normoxic Conditions Journal Of Biological Chemistry




Homework 3 1 Suppose We Have Two Four Point Sequences X N And H N As Follows A Calculate The Four Point Dft X K B Calculate The Four Point Dft Ppt Download




Hxn Ws Shouding Other Components Veswin Electronics Limited




How To Show That Y N X N H N Turns Into The Y Z X Z H Z Signal Processing Stack Exchange




Tyan Computer Barebones Fa77b7119 119f77v14hr 2t N



What Is The Nth Derivative Of X N 1 Logx Using The Leibintz Theorem Quora




1 Let X N D N 2d N 1 D N 3 And H N 2d N Chegg Com




Real Analysis Ii Chapter 9 Sequences And Series Of Functions 9 1



Www Cpp Edu Zaliyazici Ece308 Ece308 6 Pdf



Www Jstor Org Stable
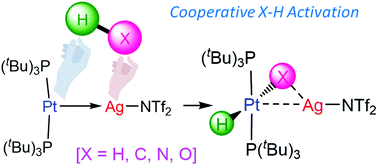



Cooperative Activation Of X H X H C O N Bonds By A Pt 0 Ag I Metal Only Lewis Pair Chemical Communications Rsc Publishing



Use The Binomial Theorem To Prove The Formula For The Derivative Of X N Stumbling Robot




If F X Sqrt X 2 1 G X X 1 X 2 1 And H X 2x 3 The



Http Www Ece Tufts Edu Ee 194nit Lect02 Pdf



1



Even More Examples




Graphing Parabolas




Ex 13 1 32 If F X Mx 2 N Nx M Nx 3 M For What M And N



Http Www Pstcc Edu Facstaff Rtjackso Math1910 Notes Continuity Pdf



コメント
コメントを投稿